Background

This wiki contains a summary of the article accepted as a tutorial for IEEE Robotics and Automation Magazine on the 4th June 2012.

Background and terminology

A rigid body is an idealization of a solid body of infinite or finite size in which deformation is neglected. We often abbreviate “rigid body” to “body”, and denotes it by the symbol $\mathcal{A}$. A body in three-dimensional space has six degrees of freedom: three degrees of freedom in translation and three in rotation. The subspace of all body motions that involve only changes in the orientation is often denoted by SO(3) (the Special Orthogonal group in three-dimensional space). It forms a group under the operation of composition of relative motion. The space of all body motions, including translations, is denoted by SE(3) (the Special Euclidean group in three-dimensional space).

A general six-dimensional displacement between two bodies is called a (relative) pose: it contains both the position and orientation. Remark that the position, orientation, and pose of a body are not absolute concepts, since they imply a second body with respect to which they are defined. Hence, only the relative position, orientation, and pose between two bodies are relevant geometric relations.

A general six-dimensional velocity between two bodies is called a (relative) twist: it contains both the rotational and the translational velocity. Similar to the position, orientation, and pose, the translational velocity, rotational velocity, and twist of a body are not absolute concepts, since they imply a second body with respect to which they are defined. Hence, only the relative translational velocity, rotational velocity, and twist between two bodies are relevant geometric relations.

When doing actual calculations with the geometric relations between rigid bodies, one has to use the coordinate representation of the geometric relations, and therefore has to choose a coordinate frame in which the coordinates are expressed in order to obtain numerical values for the geometric relations.

Semantics

Geometric primitives

The geometric relations between bodies are described using a set of geometric primitives:
  • A (spatial) point is the primitive to represent the position of a body. Points have neither volume, area, length, nor any other higher dimensional analogue. We denote points by the symbols $a$, $b$, ...
  • A vector is the geometric primitive that connects a point $a$ to a point $b$. It has a magnitude (the straight-line distance between the two points), and a direction (from $a$ to $b$). To express the magnitude of a vector, a (length) scale must be chosen.
  • An orientation frame represents an orientation, by means of three orthonormal vectors indicating the frame’s X-axis $X$, Y-axis $Y$ , and Z-axis $Z$. We denote orientation frames by the symbols $\left[a\right]$, $\left[b\right]$, ...
  • A (displacement) frame represents position and orientation of a body, by means of an orientation frame and a point (which is the orientation frame’s origin). We denote frames by the symbols $\left\{a\right\}$, $\left\{b\right\}$, ...

Each of these geometric primitives can be fixed to a body, which means that the geometric primitive coincides with the body not only instantaneously, but also over time. For the point $a$ and the body $\mathcal{C}$ for instance, this is written as $a|\mathcal{C}$. The figure below presents the geometric primitives body, point, vector, orientation frame, and frame graphically.

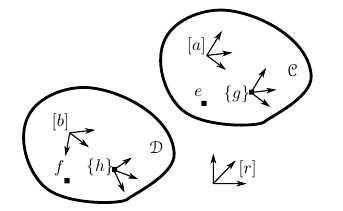Geometric PrimitivesGeometric Primitives

Geometric relations

The table below summarizes the semantics for the following geometric relations between rigid bodies: position, orientation, pose, translational velocity, rotational velocity, and twist.

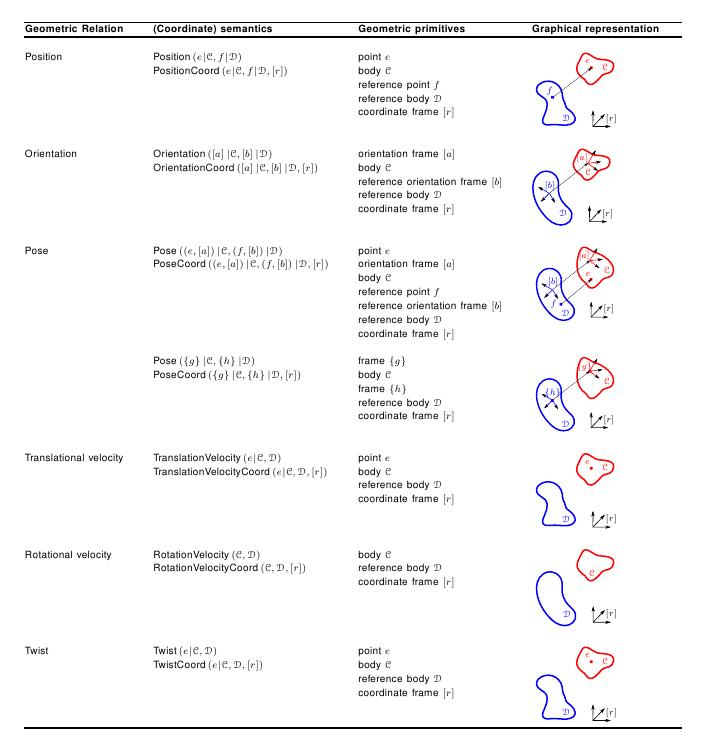Geometric relationsGeometric relations

Force, Torque, and Wrench

Screw theory, the algebra and calculus of pairs of vectors that arise in the kinematics and dynamics of rigid bodies, shows the duality between wrenches, consisting of the torque and force vectors, and twists, consisting of translational and rotational velocity vectors. The parallelism between translational, rotational velocity, and twist on the one hand, and torque, force, and wrench on the other hand, is directly reflected in the semantic representation (see the table below) and the coordinate representations.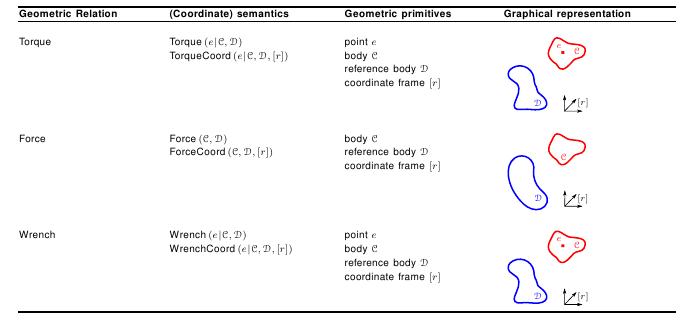

Geometric relations force, torque, and wrenchGeometric relations force, torque, and wrench