Geometric relations semantics
Remark that this wiki contains a summary of the theoretical article and the software article both published as a tutorial for IEEE Robotics and Automation Magazine:
|
The geometric relations semantics software (C++) implements the geometric relation semantics theory, hereby offering support for semantic checks for your rigid body relations calculations. This will avoid commonly made errors, and hence reduce application and, especially, system integration development time considerably. The proposed software is to our knowledge the first to offer a semantic interface for geometric operation software libraries.
The screenshot below shows the output of the semantic checks of the (wrong) composition of two positions and two orientations.
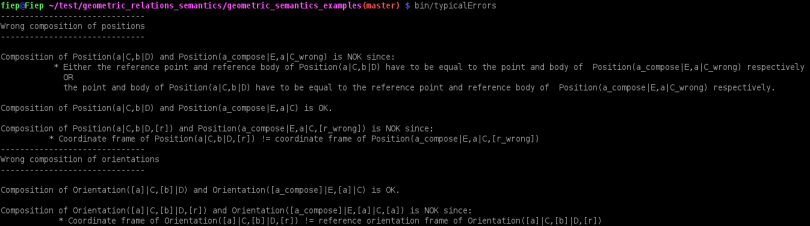Output of the semantic checks of the (wrong) composition of two positions and two orientations
The goal of the software is to provide semantic checking for calculations with geometric relations between rigid bodies on top of existing geometric libraries, which are only working on specific coordinate representations. Since there are already a lot of libraries with good support for geometric calculations on specific coordinate representations (The Orocos Kinematics and Dynamics library, the ROS geometry library, boost, ...) we do not want to design yet another library but rather will extend these existing geometric libraries with semantic support. The effort to extend an existing geometric library with semantic support is very limited: it boils down to the implementation of about six function template specializations.
What is it?
This wiki contains a summary of the article accepted as a tutorial for IEEE Robotics and Automation Magazine on the 4th June 2012.
Rigid bodies are essential primitives in the modelling of robotic devices, tasks and perception, starting with the basic geometric relations such as relative position, orientation, pose, translational velocity, rotational velocity, and twist. This wiki elaborates on the background and the software for the semantics underlying rigid body relationships. This wiki is based on the research of the KU Leuven robotics group, in this case mainly conducted by Tinne De Laet, to explain semantics of all coordinate-invariant properties and operations, and, more importantly, to document all the choices that are made in coordinate representations of these geometric relations. This resulted in a set of concrete suggestions for standardizing terminology and notation, and software with a fully unambiguous software interface, including automatic checks for semantic correctness of all geometric operations on rigid-body coordinate representations.
The geometric relations semantics software prevents commonly made errors in geometric rigid-body relations calculations like:
- Logic errors in geometric relation calculations: A lot of logic errors can occur during geometric relation calculations. For instance (there is no need to understand the details just have a look at the difference in syntax), the inverse of $\textrm{Position} \left(e|\mathcal{C}, f |\mathcal{D}\right)$ is $\textrm{Position} \left(f|\mathcal{D}, e |\mathcal{C}\right)$, while the inverse of the translational velocity $\textrm{TranslationVelocity} \left(e|\mathcal{C}, \mathcal{D}\right)$ is $\textrm{TranslationVelocity} \left(e|\mathcal{D}, \mathcal{C}\right)$. When using the semantic representation proposed in this paper, the semantics of the inverse geometric relation can be automatically derived from the forward geometric relation, preventing logic errors. A second example emerges when composing the relations involving three rigid bodies: in order to get the geometric relation of $\mathcal{C}$ with respect to body $\mathcal{D}$ one can compose the geometric relation between $\mathcal{C}$ and third body $\mathcal{E}$ with the geometric relation between body $\mathcal{E}$ and the body $\mathcal{D}$ (and not the geometric relation between the body $\mathcal{D}$ and the body $\mathcal{E}$ for instance). Such a logic constraint can be checked easily by including, for instance, the body and reference body in the semantic representation of the geometric relations.
- Composition of twists with different velocity reference point: Composing twists requires a common velocity reference point (i.e. the twists have to express the translational velocity of the same point on the body). By including the velocity reference point of the twist in the semantic representation, this constraint can be checked explicitly.
- Composition of geometric relations expressed in different coordinate frames: Composing geometric relations using coordinate representations like position vectors, translational and rotational velocity vectors, and 6D vector twists, requires that the coordinates are expressed in the same coordinate frame. By including the coordinate frame in the coordinate semantic representation of the geometric relations, this constraint can be checked explicitly.
- Composition of poses and orientation coordinate representations in wrong order: The rotation matrix and homogeneous transformation matrix coordinate representations can be composed using simple multiplication. Since matrix multiplication is however not commutative, a common error is to use a wrong multiplication order in the composition. The correct multiplication order can however be directly derived when including the bodies, frames, and points in the coordinate semantic representation of the geometric relations.
- Integration of twists when velocity reference point and coordinate frame do not belong to same frame: A twist can only be integrated when it expresses the translational velocity of the origin of the coordinate frame the twist is expressed in. When including the velocity reference point and the coordinate frame in the coordinate semantic representation of the twist, this constraint can be explicitly checked.
Background
This wiki contains a summary of the article accepted as a tutorial for IEEE Robotics and Automation Magazine on the 4th June 2012.
Background and terminology
A rigid body is an idealization of a solid body of infinite or finite size in which deformation is neglected. We often abbreviate “rigid body” to “body”, and denotes it by the symbol $\mathcal{A}$. A body in three-dimensional space has six degrees of freedom: three degrees of freedom in translation and three in rotation. The subspace of all body motions that involve only changes in the orientation is often denoted by SO(3) (the Special Orthogonal group in three-dimensional space). It forms a group under the operation of composition of relative motion. The space of all body motions, including translations, is denoted by SE(3) (the Special Euclidean group in three-dimensional space).
A general six-dimensional displacement between two bodies is called a (relative) pose: it contains both the position and orientation. Remark that the position, orientation, and pose of a body are not absolute concepts, since they imply a second body with respect to which they are defined. Hence, only the relative position, orientation, and pose between two bodies are relevant geometric relations.
A general six-dimensional velocity between two bodies is called a (relative) twist: it contains both the rotational and the translational velocity. Similar to the position, orientation, and pose, the translational velocity, rotational velocity, and twist of a body are not absolute concepts, since they imply a second body with respect to which they are defined. Hence, only the relative translational velocity, rotational velocity, and twist between two bodies are relevant geometric relations.
When doing actual calculations with the geometric relations between rigid bodies, one has to use the coordinate representation of the geometric relations, and therefore has to choose a coordinate frame in which the coordinates are expressed in order to obtain numerical values for the geometric relations.
Semantics
Geometric primitives
The geometric relations between bodies are described using a set of geometric primitives:- A (spatial) point is the primitive to represent the position of a body. Points have neither volume, area, length, nor any other higher dimensional analogue. We denote points by the symbols $a$, $b$, ...
- A vector is the geometric primitive that connects a point $a$ to a point $b$. It has a magnitude (the straight-line distance between the two points), and a direction (from $a$ to $b$). To express the magnitude of a vector, a (length) scale must be chosen.
- An orientation frame represents an orientation, by means of three orthonormal vectors indicating the frame’s X-axis $X$, Y-axis $Y$ , and Z-axis $Z$. We denote orientation frames by the symbols $\left[a\right]$, $\left[b\right]$, ...
- A (displacement) frame represents position and orientation of a body, by means of an orientation frame and a point (which is the orientation frame’s origin). We denote frames by the symbols $\left\{a\right\}$, $\left\{b\right\}$, ...
Each of these geometric primitives can be fixed to a body, which means that the geometric primitive coincides with the body not only instantaneously, but also over time. For the point $a$ and the body $\mathcal{C}$ for instance, this is written as $a|\mathcal{C}$. The figure below presents the geometric primitives body, point, vector, orientation frame, and frame graphically.
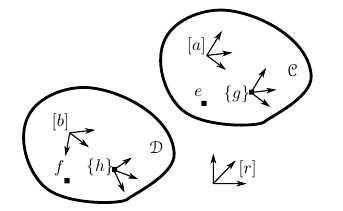Geometric Primitives
Geometric relations
The table below summarizes the semantics for the following geometric relations between rigid bodies: position, orientation, pose, translational velocity, rotational velocity, and twist.
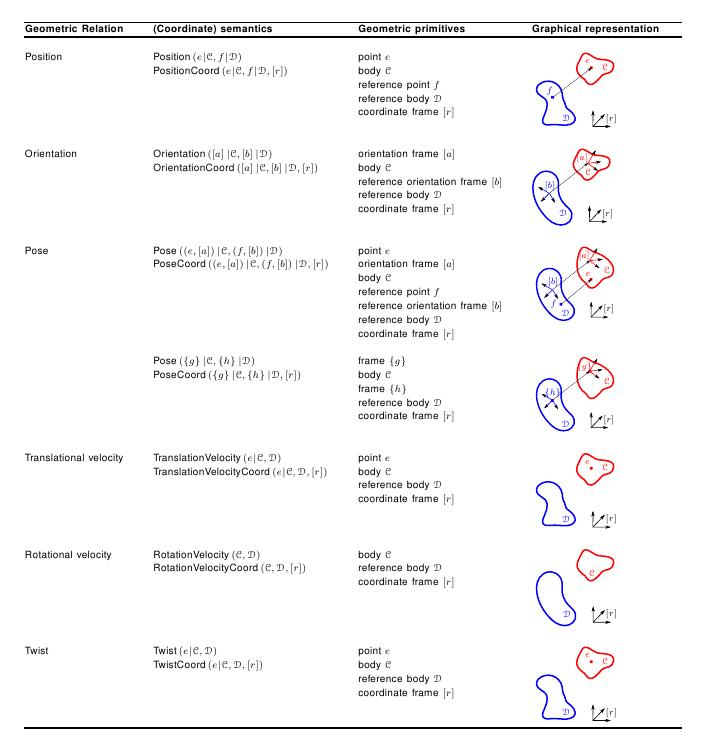Geometric relations
Force, Torque, and Wrench
Screw theory, the algebra and calculus of pairs of vectors that arise in the kinematics and dynamics of rigid bodies, shows the duality between wrenches, consisting of the torque and force vectors, and twists, consisting of translational and rotational velocity vectors. The parallelism between translational, rotational velocity, and twist on the one hand, and torque, force, and wrench on the other hand, is directly reflected in the semantic representation (see the table below) and the coordinate representations.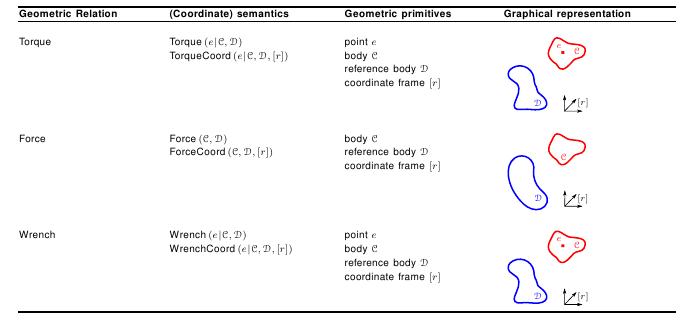
Geometric relations force, torque, and wrench
Design
- The design idea
- The design
- The software structure and content
- Core library: geometric_semantics
- KDL support: geometric_semantics_kdl
- ROS tf support: geometric_semantics_tf
- ROS messages: geometric_semantics_msgs
- ROS message conversions: geometric_semantics_msgs_conversions
- ROS tf messages support: geometric_semantics_tf_msgs
- ROS tf message conversions: geometric_semantics_tf_msgs_conversions
- Examples: geometric_semantics_examples
The software implements the geometric relation semantics, hereby offering support for semantic checks for your rigid body relations. This will avoid commonly made errors, and hence reduce application (and, especially, system integration) development time considerably. The proposed software is to our knowledge the first to offer a semantic interface for geometric operation software libraries.
The design idea
The goal of the geometric_relations_semantics library is to provide semantic checking for calculations with geometric relations between rigid bodies on top of existing geometric libraries, which are only working on specific coordinate representations. Since there are already a lot of libraries with good support for geometric calculations on specific coordinate representations (The Orocos Kinematics and Dynamics library, the ROS geometry library, boost, ...) we do not want to design yet another library but rather will extend these existing geometric libraries with semantic support. The effort to extend an existing geometric library with semantic support is very limited: it boils down to the implementation of about six function template specializations.For the semantic checking, we created the (templated) geometric_semantics core library, providing all the necessary semantic support for geometric relations (relative positions, orientations, poses, translational velocities, rotational velocities, twists, forces, torques, and wrenches) and the operations on these geometric relations (composition, integration, inversion, ...).
If you want to perform actual geometric relation calculations, you will need particular coordinate representations (for instance a homogeneous transformation matrix for a pose) and a geometric library offering support for calculations on these coordinate representations (for instance multiplication of homogeneous transformation matrices). To this end, you can build your own library depending on the geometric_semantics core library in which you implement a limited number of functions, which make the connection between semantic operations (for instance composition) and actual coordinate representation calculations (for instance multiplication of homogeneous transformation matrices). We already provide support for two geometric libraries: the Orocos Kinematics and Dynamics library and the ROS geometry library, in the geometric_semantics_kdl and geometric_semantics_tf libraries, respectively.
The design
For every geometric relation (position, orientation, pose, translational velocity, rotational velocity, twist, force, torque, and wrench) the geometric_semantics library contains four classes. Here we will explain the design with the position geometric relation, but all other geometric relations have a similar design. For the position geometric relation there are four classes:- PositionSemantics: This class contains the semantics of the (coordinate-free) Position geometric relation. For instance in this case it contains the information on the point, reference point, body, and reference body.
- PositionCoordinatesSemantics: This class contains a PositionSemantics object of the geometric relation at hand and the extra semantic information needed for semantics of position coordinate geometric relation, i.e. the coordinate frame in which the coordinates are expressed.
- PositionCoordinates: This templated class contains the actual coordinate representation of the geometric relation, for instance a position vector for the position geometric relation. The template is the actual geometry object (of an external library) you will use as a coordinate representation, for instance a KDL::Vector.
- Position: This templated class is a composition of a PositionCoordinatesSemantics object and a PositionCoordinates object. In case you want both semantic support and want to do actual geometric calculations, this is the level you will work at.
Again, the template is the actual geometry (of an external library) you will use as a coordinate representation, for instance a KDL::Vector.
The above described design is illustrated by the figure below.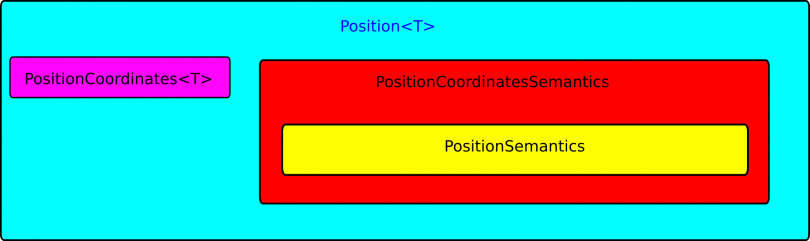 
Position geometric relation design
Remark that all four of the above 'levels' are of actual use:
- PositionSemantics: to do coordinate-free semantic checking (without actual geometric calculations);
- PositionCoordinateSemantics: to do semantic checking involving coordinate systems (without actual geometric calculations);
- PositionCoordinates: to do the actual geometric calculations; and
- Position: to do both semantic checking and the actual geometric calculations.
Pose, Twist, and Wrench
We need to give some extra information on the pose, twist, and wrench geometric relations since they can be represented as a composition of two other geometric relations (Pose = Position + Orientation, Twist = TranslationalVelocity + RotationalVelocity, Wrench = Force + Torque) or as a new geometric relation. For example we could want to use a homogeneous transformation matrix as a coordinate representation of a pose, and in this case we would also want, for efficiency reasons, to do direct calculations on the homogeneous transformation matrices. In another case we want to represent the pose as the composition of a position (with for instance a position vector as a coordinate representation) and an orientation (with for instance Euler angles as a coordinate representation). The software allows both designs as illustrated in the two figures below.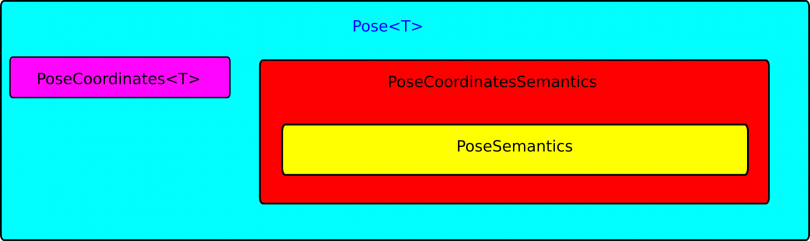
Pose geometric relation design as a basic geometric relation 
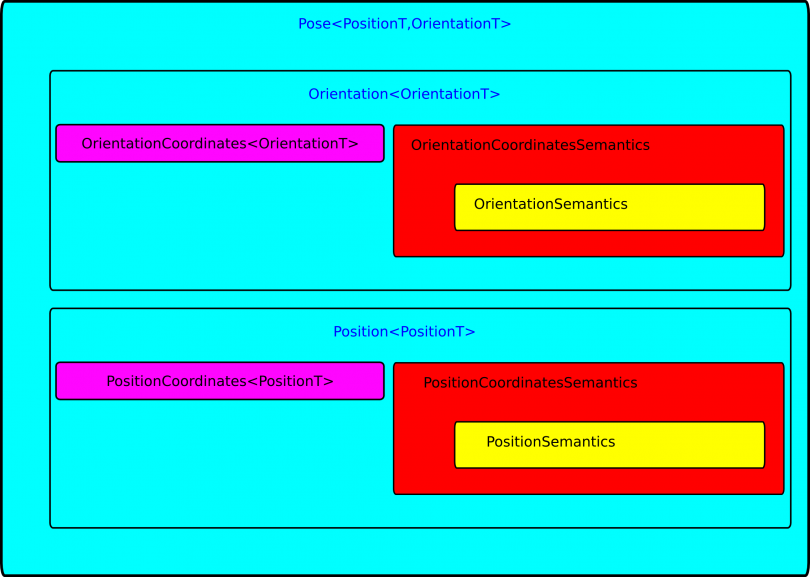Pose geometric relation design as an composition of a Position and Orientation geometric relation
The software structure and content
Core library: geometric_semantics
KDL support: geometric_semantics_kdl
ROS tf support: geometric_semantics_tf
ROS messages: geometric_semantics_msgs
ROS message conversions: geometric_semantics_msgs_conversions
ROS tf messages support: geometric_semantics_tf_msgs
ROS tf message conversions: geometric_semantics_tf_msgs_conversions
Examples: geometric_semantics_examples
API
The API is available at: http://people.mech.kuleuven.be/~tdelaet/geometric_relations_semantics/doc/.
Quick start
Overview
The framework is ordered following a OROCOS-ROS approach and consists of one stack:- geometric_relations_semantics.
This stack consists of following packages:
- geometric_semantics: geometric_semantics is the core of the geometric_relations_semantics stack and provides c++ code for the semantic support of geometric relations between rigid bodies (relative position, orientation, pose, translational velocity, rotational velocity, twist, force, torque, and wrench). If you want to use semantic checking for the geometric relation operations between rigid bodies in your application you can check the geometric_semantics_examples package. If you want to create support for your own geometry types on top of the geometric_semantics package, the geometric_semantics_kdl provides a good starting point.
- geometric_semantics_examples: geometric_semantics_examples groups some examples showing how the geometric_semantics can be used to provide semantic checking for the geometric relations between rigid bodies in your application.
- geometric_semantics_orocos_typekit: geometric_semantics_orocos_typekit provides Orocos typekit support for the geometric_semantics types, such that the geometric semantics types are visible within Orocos (in the TaskBrowser component, in Orocos script, reporting, reading and writing to files (for instance for properties), ... ).
- geometric_semantics_orocos_typekit_kdl: geometric_semantics_orocos_typekit_kdl provides Orocos typekit support for geometric semantics coordinate representations using KDL types.
- geometric_semantics_msgs: geometric_semantics_msgs provides ROS messages matching the C++ types defined on the geometric_semantics package, in order to support semantic support during message based communication.
- geometric_semantics_msgs_conversions: geometric_semantics_msgs_conversions provides support conversions between geometric_semantics_msgs and the C++ geometric_semantics types defined on the geometric_semantics package.
- geometric_semantics_msgs_kdl: geometric_semantics_kdl provides support for orocos_kdl types on top of the geometric_semantics package (for instance KDL::Frame to represent the relative pose of two rigid bodies). If you want to create support for your own geometry types on top of the geometric_semantics package, this package provides a good starting point.
- geometric_semantics_msgs_tf: geometric_semantics_tf provides support for tf datatypes (see http://www.ros.org/wiki/tf/Overview/Data%20Types) on top of the geometric_semantics package (for instance tf::Pose to represent the relative pose of two rigid bodies).
- geometric_semantics_tf_msgs: geometric_semantics_tf_msgs provides ROS messages matching the C++ types defined on the geometric_semantics_tf package, in order to support semantic support for tf types during message based communication.
- geometric_semantics_tf_msgs_conversions: geometric_semantics_tf_msgs_conversions provides support conversions between geometric_semantics_tf_msgs and the C++ geometric_semantics_tf types defined on the geometric_semantics_tf package.
Each package contains the following subdirectories:
- src/ containing the source code of the components (mainly C++ or python for the ROS msgs support).
Installation instructions
Warning, so far we only provide support for linux-based systems. For Windows or Mac, you're still at your own, but we are always interested in your experiences and in extensions of the installation instructions, quick start guide, and user guide.Dependencies
- Boost version 1.42 or up (for ubuntu you can use the libboost1.4*-dev libraries)
- Orocos Kinematics and Dynamics Library 0.2.3 and up. For more information visit the Orocos website
- rtt_geometry stack: the Orocos typekit support for KDL types, introduces a dependency on the kdl_typekit
- ROS Electric/Fuerte/Groovy: optional unless you want to use the PR2, but highly recommended: build system and tools like rospack find are practical and are used in the example scripts
- ros_comm
- geometry
- common_msgs
Compiling from source
- First you should get the sources from git using:
git clone https://gitlab.mech.kuleuven.be/rob-dsl/geometric-relations-semantics.git
- Go into the geometric_relations_semantics directory using:
cd geometric_relations_semantics
- Add this directory to your ROS_PACKAGE_PATH environment variable using:
export ROS_PACKAGE_PATH=$PWD:$ROS_PACKAGE_PATH
- Install the dependencies and build the library using:
rosdep install geometric_relations_semantics rosmake geometric_relations_semantics
- Everything should compile out of the box, and you are now ready to start using geometric relation semantics support.
- If you want to run the test of the packages you should use for instance (for the geometric_semantics core package):
roscd geometric_semantics make test
Setup
It is strongly recommended that you add the geometric_relations_semantics directory to your ROS_PACKAGE_PATH in your .bashrc file.(Re)building the stack or individual packages
- To build the geometric_relations_semantics stack use:
rosmake geometric_relations_semantics
- You can also (re)build any package individually using:
rosmake PACKAGE_NAME
Running the tests
- If you want to run the test of the packages you should for go to the package for instance (for the geometric_semantics core package):
roscd geometric_semantics
- And next make and run the tests:
make test
User guide
If you are looking for installation instructions you should read the quick start.
Setting the build options of the core library
You can customize the behavior of the semantic checking (checking or not, and screen output or not) by changing the build options of the geometric_semantics library (see CMakeLists.txt of geometric_semantics package)- add_definitions(-DCHECK): when using this build flag, the semantic checking will be enabled.
- add_definitions(-DOUTPUT_CORRECT): when using this build flag, you will get screen output for operations that are semantically correct.
- add_definitions(-DOUTPUT_WRONG): when using this build flag, you will get screen output for operations that are semantically wrong.
Using the geometric relations semantics in your own application
Here we will explain how you can use the geometric relations semantics in your application, in particular using the Orocos Kinematics and Dynamics library as a geometry library, supplemented with the semantic support.
Preparing your own application using the ROS-build system
- Create a new ROS package (in this case with name myApplication), with a dependency on the geometric_semantics_kdl:
roscreate-pkg myApplication geometric_semantics_kdlThis will automatically create a directory with name myApplication and a basic build infrastructure (see the roscreate-pkg documentation)
- Add the newly created directory to your ROS_PACKAGE_PATH environment variable:
cd myApplication export ROS_PACKAGE_PATH=$PWD:$ROS_PACKAGE_PATH
Writing your own application
- Go to the application directory:
roscd myApplication
- Create a main C++ file
touch myApplication.cpp- Edit the C++ file with your favorite editor
- Include the necessary headers. For instance:
#include <Pose/Pose.h> #include <Pose/PoseCoordinatesKDL.h>
- It can be convenient to use the geometric_semantics namespace and for instance the one of your geometry library (in this case KDL):
using namespace geometric_semantics; using namespace KDL;
- In your main you should create the necessary geometric relations. For instance for a pose, first create the KDL coordinates:
Rotation coordinatesRotB2_B1=Rotation::EulerZYX(M_PI,0,0); Vector coordinatesPosB2_B1(2.2,0,0); KDL::Frame coordinatesFrameB2_B1(coordinatesRotB2_B1,coordinatesPosB2_B1)
Then use this KDL coordinates to create a PoseCoordinates object:
PoseCoordinates<KDL::Frame> poseCoordB2_B1(coordinatesFrameB2_B1);
Then create a Pose object using both the semantic information and the PoseCoordinates:
Pose<KDL::Frame> poseB2_B1("b2","b2","B2","b1","b1","B1","b1",poseCoordB2_B1);
- Now you are ready to do actual calculations using semantic checking. For instance to take the inverse:
Pose<KDL::Frame> poseB1_B2 = poseB2_B1.inverse()
Building your own application
- To build you application you should edit the CMakeLists.txt file created in you application directory. Add the your C++ main file to be build as an executable adding the following line:
rosbuild_add_executable(myApplication myApplication.cpp)
- Now you are ready to build, so type
rosmake myApplication
and the executable will be created in the bin directory.
- To run the executable do:
bin/myApplicationYou will get the semantic output on your screen.
Extending your geometry library with semantic checking
Imagine you have your own geometry library with support for geometric relation coordinate representations and calculations with these coordinate representations. You however would like to have semantic support on top of this geometry library. Probably the best thing to do in this case is to mimic our support for the Orocos Kinematics and Dynamics Library. To have a look at it do:
roscd geometric_semantics_kdl/Template specialization
The only thing you have to do is write template specializations. So for instance to get support for KDL::Rotation, which is a coordinate representation for a Orientation geometric relation, you have to write the template specialization for OrientationCoordinates<T>, i.e. OrientationCoordinates<KDL::Rotation>.Semantic constraints invoked by your coordinate representations
The first thing to find out is which semantic constraints are invoked by the particular coordinate representation you use. For instance a KDL::Rotation represents a 3x3 rotation matrix and invokes the semantic constraint that the reference orientation frame is equal to the coordinate frame.The possible semantic constraints are listed in the *Coordinates.h files in the geometric_semantics core library. So for instance for OrientationCoordinates we find there an enumeration of the different possible semantic constraints imposed by Orientation coordinate representations:
/** *\brief Constraints imposed by the orientation coordinate representation to the semantics */ enum Constraints{ noConstraints = 0x00, coordinateFrame_equals_referenceOrientationFrame = 0x01, // constraint that the orientation frame on the reference body has to be equal to the coordinate frame };
You should specify the constraint when writing the template specialization of the OrientationCoordinates<KDL::Rotation>:
// template specialization for KDL::Rotation template <> OrientationCoordinates<KDL::Rotation>::OrientationCoordinates(const KDL::Rotation& coordinates): data(coordinates), constraints(coordinateFrame_equals_referenceOrientationFrame){ };
Specializing other functions to do actual coordinate calculations
The other function template specializations specify the actual coordinate calculations that have to be performed for semantic operations like inverse, changing the coordinate frame, changing the orientation frame, ... For instance, to specialize the inverse for KDL::Rotation coordinate representations:
template <> OrientationCoordinates<KDL::Rotation> OrientationCoordinates<KDL::Rotation>::inverse2Impl() const { return OrientationCoordinates<KDL::Rotation>(this->data.Inverse()); }
Tutorials
Setting up a package and the build system for your application
This tutorial explains (one possibility) to set up a build system for your application using the geometric_relations_semantics. The possibility we explain uses the ROS package and build infrastructure, and will therefore assume you have ROS installed and set up on your computer.
- Create a new ROS package (in this case with name myApplication), with a dependency on the geometric_semantics library and for instance the geometric_semantics_kdl library:
roscreate-pkg myApplication geometric_semantics geometric_semantics_kdl
This will automatically create a directory with name myApplication and a basic build infrastructure (see the roscreate-pkg documentation)
- Add the newly created directory to your ROS_PACKAGE_PATH environment variable:
export ROS_PACKAGE_PATH=myApplication:$ROS_PACKAGE_PATH
Your first application using semantic checking on geometric relations (without coordinate checking)
This tutorial assumes you have prepared a ROS package with name myApplication and that you have set your ROS_PACKAGE_PATH environment variable accordingly, as explained in this tutorial.
In this tutorial we first explain how you can create basic semantic objects (without coordinates and coordinate checking) and perform semantic operations on them. We will show how you can create any of the supported geometric relations: position, orientation, pose, transational velocity, rotational velocity, twist, force, torque, and wrench.
Remark that the file resulting from following this tutorial is attached to this wiki page for completeness.
Prepare the main file
- Go to the directory of our first application using:
roscd myApplication
- Create a main file (in this tutorial called myFirstApplication.cpp) in which we will put the code of our first application.
touch myFirstApplication.cpp- Edit the C++ file with your favorite editor. For instance:
vim myFirstApplication.cpp- Include the necessary headers.
#include <Position/PositionSemantics.h> #include <Orientation/OrientationSemantics.h> #include <Pose/PoseSemantics.h> #include <LinearVelocity/LinearVelocitySemantics.h> #include <AngularVelocity/AngularVelocitySemantics.h> #include <Twist/TwistSemantics.h> #include <Force/ForceSemantics.h> #include <Torque/TorqueSemantics.h> #include <Wrench/WrenchSemantics.h>
- Next we use the geometric_semantics namespace for convenience:
using namespace geometric_semantics;
- Create a main program:
int main (int argc, const char* argv[]) { // Here comes the code of our first application }
Building your first application
- To build you application you should edit the CMakeLists.txt file created in your application directory.
vim CMakeLists.txt- Add the C++ main file to be build as an executable by adding the following line:
rosbuild_add_executable(myFirstApplication myFirstApplication.cpp)
- Now you are ready to build, so type
rosmake myApplication
and the executable will be created in the bin directory.
- To run the executable do:
bin/myFirstApplicationYou will get the semantic output on your screen.
Creating the geometric relations semantics
- We will start with creating the geometric relation semantics objects for the relation between body C with point a and orientation frame [e], and body D with point b and orientation frame [f]:
// Creating the geometric relations semantics PositionSemantics position("a","C","b","D"); OrientationSemantics orientation("e","C","f","D"); PoseSemantics pose("a","e","C","b","f","D"); LinearVelocitySemantics linearVelocity("a","C","D"); AngularVelocitySemantics angularVelocity("C","D"); TwistSemantics twist("a","C","D"); TorqueSemantics torque("a","C","D"); ForceSemantics force("C","D"); WrenchSemantics wrench("a","C","D");
Doing semantic operations
- We can for instance take the inverses of the created semantic geometric relations by:
//Doing semantic operations with the geometric relations // inverting PositionSemantics positionInv = position.inverse(); OrientationSemantics orientationInv = orientation.inverse(); PoseSemantics poseInv = pose.inverse(); LinearVelocitySemantics linearVelocityInv = linearVelocity.inverse(); AngularVelocitySemantics angularVelocityInv = angularVelocity.inverse(); TwistSemantics twistInv = twist.inverse(); TorqueSemantics torqueInv = torque.inverse(); ForceSemantics forceInv = force.inverse(); WrenchSemantics wrenchInv = wrench.inverse();
std::cout << "-----------------------------------------" << std::endl; std::cout << "Inverses: " << std::endl; std::cout << " " << positionInv << " is the inverse of " << position << std::endl; std::cout << " " << orientationInv << " is the inverse of " << orientation << std::endl; std::cout << " " << poseInv << " is the inverse of " << pose << std::endl; std::cout << " " << linearVelocityInv << " is the inverse of " << linearVelocity << std::endl; std::cout << " " << angularVelocityInv << " is the inverse of " << angularVelocity << std::endl; std::cout << " " << twistInv << " is the inverse of " << twist << std::endl; std::cout << " " << torqueInv << " is the inverse of " << torque << std::endl; std::cout << " " << forceInv << " is the inverse of " << force << std::endl; std::cout << " " << wrenchInv << " is the inverse of " << wrench << std::endl;
- Now we can for instance compose the result with their inverses. Mind that the order of composition does not matter, since this is automatically derived from the semantic information in the objects.
//Composing PositionSemantics positionComp = compose(position,positionInv); OrientationSemantics orientationComp = compose(orientation,orientationInv); PoseSemantics poseComp = compose(pose,poseInv); LinearVelocitySemantics linearVelocityComp = compose(linearVelocity,linearVelocityInv); AngularVelocitySemantics angularVelocityComp = compose(angularVelocity,angularVelocityInv); TwistSemantics twistComp = compose(twist,twistInv); TorqueSemantics torqueComp = compose(torque,torqueInv); ForceSemantics forceComp = compose(force,forceInv); WrenchSemantics wrenchComp = compose(wrench,wrenchInv);
std::cout << "-----------------------------------------" << std::endl; std::cout << "Composed objects: " << std::endl; std::cout << " " << positionComp << " is the composition of " << position << " and " << positionInv << std::endl; std::cout << " " << orientationComp << " is the composition of " << orientation << " and " << orientationInv << std::endl; std::cout << " " << poseComp << " is the composition of " << pose << " and " << poseInv << std::endl; std::cout << " " << linearVelocityComp << " is the composition of " << linearVelocity << " and " << linearVelocityInv << std::endl; std::cout << " " << angularVelocityComp << " is the composition of " << angularVelocity << " and " << angularVelocityInv << std::endl; std::cout << " " << twistComp << " is the composition of " << twist << " and " << twistInv << std::endl; std::cout << " " << torqueComp << " is the composition of " << torque << " and " << torqueInv << std::endl; std::cout << " " << forceComp << " is the composition of " << force << " and " << forceInv << std::endl; std::cout << " " << wrenchComp << " is the composition of " << wrench << " and " << wrenchInv << std::endl;
| Attachment | Size |
|---|---|
| myFirstApplication.cpp | 4.28 KB |
Your second application using semantic checking on geometric relations including coordinate checking
This tutorial assumes you have prepared a ROS package with name myApplication and that you have set your ROS_PACKAGE_PATH environment variable accordingly, as explained in this tutorial.
In this tutorial we first explain how you can create basic semantic objects (without coordinates but with coordinate checking) and perform semantic operations on them. We will show how you can create any of the supported geometric relations: position, orientation, pose, transational velocity, rotational velocity, twist, force, torque, and wrench.
Remark that the file resulting from following this tutorial is attached to this wiki page for completeness.
Prepare the main file
- Prepare a mySecondApplication.cpp main file as explained in this tutorial.
- Edit the C++ file with your favorite editor. For instance:
vim mySecondApplication.cpp- Include the necessary headers.
#include <Position/PositionCoordinatesSemantics.h> #include <Orientation/OrientationCoordinatesSemantics.h> #include <Pose/PoseCoordinatesSemantics.h> #include <LinearVelocity/LinearVelocityCoordinatesSemantics.h> #include <AngularVelocity/AngularVelocityCoordinatesSemantics.h> #include <Twist/TwistCoordinatesSemantics.h> #include <Force/ForceCoordinatesSemantics.h> #include <Torque/TorqueCoordinatesSemantics.h> #include <Wrench/WrenchCoordinatesSemantics.h>
- Next we use the geometric_semantics namespace for convenience:
using namespace geometric_semantics;
- Create a main program:
int main (int argc, const char* argv[]) { // Here comes the code of our second application }
Building your second application
- To build you application you should edit the CMakeLists.txt file created in you application directory. Add the your C++ main file to be build as an executable adding the following line:
rosbuild_add_executable(mySecondApplication mySecondApplication.cpp)
- Now you are ready to build, so type
rosmake myApplication
and the executable will be created in the bin directory.
- To run the executable do:
bin/mySecondApplicationYou will get the semantic output on your screen.
Creating the geometric relations coordinates semantics
- We will start with creating the geometric relation coordinates semantics objects for the relation between body C with point a and orientation frame [e], and body D with point b and orientation frame [f], all expressed in coordinate frame [r]:
// Creating the geometric relations coordinates semantics PositionCoordinatesSemantics position("a","C","b","D","r"); OrientationCoordinatesSemantics orientation("e","C","f","D","r"); PoseCoordinatesSemantics pose("a","e","C","b","f","D","r"); LinearVelocityCoordinatesSemantics linearVelocity("a","C","D","r"); AngularVelocityCoordinatesSemantics angularVelocity("C","D","r"); TwistCoordinatesSemantics twist("a","C","D","r"); TorqueCoordinatesSemantics torque("a","C","D","r"); ForceCoordinatesSemantics force("C","D","r"); WrenchCoordinatesSemantics wrench("a","C","D","r");
Doing semantic coordinate operations
- We can for instance take the inverses of the created geometric relation coordinates semantics by:
//Doing semantic operations with the geometric relations // inverting PositionCoordinatesSemantics positionInv = position.inverse(); OrientationCoordinatesSemantics orientationInv = orientation.inverse(); PoseCoordinatesSemantics poseInv = pose.inverse(); LinearVelocityCoordinatesSemantics linearVelocityInv = linearVelocity.inverse(); AngularVelocityCoordinatesSemantics angularVelocityInv = angularVelocity.inverse(); TwistCoordinatesSemantics twistInv = twist.inverse(); TorqueCoordinatesSemantics torqueInv = torque.inverse(); ForceCoordinatesSemantics forceInv = force.inverse(); WrenchCoordinatesSemantics wrenchInv = wrench.inverse();
std::cout << "-----------------------------------------" << std::endl; std::cout << "Inverses: " << std::endl; std::cout << " " << positionInv << " is the inverse of " << position << std::endl; std::cout << " " << orientationInv << " is the inverse of " << orientation << std::endl; std::cout << " " << poseInv << " is the inverse of " << pose << std::endl; std::cout << " " << linearVelocityInv << " is the inverse of " << linearVelocity << std::endl; std::cout << " " << angularVelocityInv << " is the inverse of " << angularVelocity << std::endl; std::cout << " " << twistInv << " is the inverse of " << twist << std::endl; std::cout << " " << torqueInv << " is the inverse of " << torque << std::endl; std::cout << " " << forceInv << " is the inverse of " << force << std::endl; std::cout << " " << wrenchInv << " is the inverse of " << wrench << std::endl;
- Now we can for instance compose the result with their inverses. Mind that the order of composition does not matter, since this is automatically derived from the semantic information in the objects.
//Composing PositionCoordinatesSemantics positionComp = compose(position,positionInv); OrientationCoordinatesSemantics orientationComp = compose(orientation,orientationInv); PoseCoordinatesSemantics poseComp = compose(pose,poseInv); LinearVelocityCoordinatesSemantics linearVelocityComp = compose(linearVelocity,linearVelocityInv); AngularVelocityCoordinatesSemantics angularVelocityComp = compose(angularVelocity,angularVelocityInv); TwistCoordinatesSemantics twistComp = compose(twist,twistInv); TorqueCoordinatesSemantics torqueComp = compose(torque,torqueInv); ForceCoordinatesSemantics forceComp = compose(force,forceInv); WrenchCoordinatesSemantics wrenchComp = compose(wrench,wrenchInv);
std::cout << "-----------------------------------------" << std::endl; std::cout << "Composed objects: " << std::endl; std::cout << " " << positionComp << " is the composition of " << position << " and " << positionInv << std::endl; std::cout << " " << orientationComp << " is the composition of " << orientation << " and " << orientationInv << std::endl; std::cout << " " << poseComp << " is the composition of " << pose << " and " << poseInv << std::endl; std::cout << " " << linearVelocityComp << " is the composition of " << linearVelocity << " and " << linearVelocityInv << std::endl; std::cout << " " << angularVelocityComp << " is the composition of " << angularVelocity << " and " << angularVelocityInv << std::endl; std::cout << " " << twistComp << " is the composition of " << twist << " and " << twistInv << std::endl; std::cout << " " << torqueComp << " is the composition of " << torque << " and " << torqueInv << std::endl; std::cout << " " << forceComp << " is the composition of " << force << " and " << forceInv << std::endl; std::cout << " " << wrenchComp << " is the composition of " << wrench << " and " << wrenchInv << std::endl;
| Attachment | Size |
|---|---|
| mySecondApplication.cpp | 4.72 KB |
Your third application doing actual geometric calculations on top of the semantic checking
This tutorial assumes you have prepared a ROS package with name myApplication and that you have set your ROS_PACKAGE_PATH environment variable accordingly, as explained in this tutorial.
In this tutorial we first explain how you can create full geometric relation objects (with semantics and actual coordinate representation) and perform operations on them. We will show how you can create any of the supported geometric relations: position, orientation, pose, transational velocity, rotational velocity, twist, force, torque, and wrench. To this end we will use the coordinate representations of the Orocos Kinematics and Dynamics Library. The semantic support on top of this geometry library is already provided by the geometric_semantics_kdl package.
Remark that the file resulting from following this tutorial is attached to this wiki page for completeness.
Prepare the main file
- Prepare a myThirdApplication.cpp main file as explained in this tutorial.
- Edit the C++ file with your favorite editor. For instance:
vim myThirdApplication.cpp- Include the necessary headers
#include <Position/Position.h> #include <Orientation/Orientation.h> #include <Pose/Pose.h> #include <LinearVelocity/LinearVelocity.h> #include <AngularVelocity/AngularVelocity.h> #include <Twist/Twist.h> #include <Force/Force.h> #include <Torque/Torque.h> #include <Wrench/Wrench.h> #include <Position/PositionCoordinatesKDL.h> #include <Orientation/OrientationCoordinatesKDL.h> #include <Pose/PoseCoordinatesKDL.h> #include <LinearVelocity/LinearVelocityCoordinatesKDL.h> #include <AngularVelocity/AngularVelocityCoordinatesKDL.h> #include <Twist/TwistCoordinatesKDL.h> #include <Force/ForceCoordinatesKDL.h> #include <Torque/TorqueCoordinatesKDL.h> #include <Wrench/WrenchCoordinatesKDL.h> #include <kdl/frames.hpp> #include <kdl/frames_io.hpp>
- Next we use the geometric_semantics namespace and the KDL namespace for convenience:
using namespace geometric_semantics; using namespace KDL;
- Create a main program:
int main (int argc, const char* argv[]) { // Here goes the code of our third application }
Building your Third application
- To build you application you should edit the CMakeLists.txt file created in you application directory. Add the your C++ main file to be build as an executable adding the following line:
rosbuild_add_executable(myThirdApplication myThirdApplication.cpp)
- Now you are ready to build, so type
rosmake myApplication
and the executable will be created in the bin directory.
- To run the executable do:
bin/myThirdApplicationYou will get the semantic output on your screen.
Creating the geometric relations
- We will start with creating the geometric relation objects for the relation between body C with point a and orientation frame [e], and body D with point b and orientation frame [f], all expressed in coordinate frame [r], together with their coordinate representations using KDL types.
// Creating the geometric relations // a Position with a KDL::Vector Vector coordinatesPosition(1,2,3); Position<Vector> position("a","C","b","D","r",coordinatesPosition); // an Orientation with KDL::Rotation Rotation coordinatesOrientation=Rotation::EulerZYX(M_PI/4,0,0); Orientation<Rotation> orientation("e","C","f","D","f",coordinatesOrientation); // a Pose with a KDL::Frame KDL::Frame coordinatesPose(coordinatesOrientation,coordinatesPosition); Pose<KDL::Frame> pose1("a","e","C","b","f","D","f",coordinatesPose); // a Pose as aggregation of a Position and a Orientation Pose<Vector,Rotation> pose2(position,orientation); // a LinearVelocity with a KDL::Vector Vector coordinatesLinearVelocity(1,2,3); LinearVelocity<Vector> linearVelocity("a","C","D","r",coordinatesLinearVelocity); // a AngularVelocity with a KDL::Vector Vector coordinatesAngularVelocity(1,2,3); AngularVelocity<Vector> angularVelocity("C","D","r",coordinatesAngularVelocity); // a Twist with a KDL::Twist KDL::Twist coordinatesTwist(coordinatesLinearVelocity,coordinatesAngularVelocity); geometric_semantics::Twist<KDL::Twist> twist1("a","C","D","r",coordinatesTwist); // a Twist of a LinearVelocity and a AngularVelocity geometric_semantics::Twist<Vector,Vector> twist2(linearVelocity,angularVelocity); // a Torque with a KDL::Vector Vector coordinatesTorque(1,2,3); Torque<Vector> torque("a","C","D","r",coordinatesTorque); // a Force with a KDL::Vector Vector coordinatesForce(1,2,3); Force<Vector> force("C","D","r",coordinatesForce); // a Wrench with a KDL::Wrench KDL::Wrench coordinatesWrench(coordinatesForce,coordinatesTorque); geometric_semantics::Wrench<KDL::Wrench> wrench1("a","C","D","r",coordinatesWrench); // a Wrench of a Force and a Torque geometric_semantics::Wrench<KDL::Vector,KDL::Vector> wrench2(torque,force);
Doing geometric operations
- We can for instance take the inverses of the created geometric relation by:
//Doing operations with the geometric relations // inverting Position<Vector> positionInv = position.inverse(); Orientation<Rotation> orientationInv = orientation.inverse(); Pose<KDL::Frame> pose1Inv = pose1.inverse(); Pose<Vector,Rotation> pose2Inv = pose2.inverse(); LinearVelocity<Vector> linearVelocityInv = linearVelocity.inverse(); AngularVelocity<Vector> angularVelocityInv = angularVelocity.inverse(); geometric_semantics::Twist<KDL::Twist> twist1Inv = twist1.inverse(); geometric_semantics::Twist<Vector,Vector> twist2Inv = twist2.inverse(); Torque<Vector> torqueInv = torque.inverse(); Force<Vector> forceInv = force.inverse(); geometric_semantics::Wrench<KDL::Wrench> wrench1Inv = wrench1.inverse(); geometric_semantics::Wrench<Vector,Vector> wrench2Inv = wrench2.inverse();
// print the inverses std::cout << "-----------------------------------------" << std::endl; std::cout << "Inverses: " << std::endl; std::cout << " " << positionInv << " is the inverse of " << position << std::endl; std::cout << " " << orientationInv << " is the inverse of " << orientation << std::endl; std::cout << " " << pose1Inv << " is the inverse of " << pose1 << std::endl; std::cout << " " << pose2Inv << " is the inverse of " << pose2 << std::endl; std::cout << " " << linearVelocityInv << " is the inverse of " << linearVelocity << std::endl; std::cout << " " << angularVelocityInv << " is the inverse of " << angularVelocity << std::endl; std::cout << " " << twist1Inv << " is the inverse of " << twist1 << std::endl; std::cout << " " << twist2Inv << " is the inverse of " << twist2 << std::endl; std::cout << " " << torqueInv << " is the inverse of " << torque << std::endl; std::cout << " " << forceInv << " is the inverse of " << force << std::endl; std::cout << " " << wrench1Inv << " is the inverse of " << wrench1 << std::endl; std::cout << " " << wrench2Inv << " is the inverse of " << wrench2 << std::endl;
- Now we can for instance compose the result with their inverses. Mind that the order of composition does not matter, since this is automatically derived from the semantic information in the objects.
//Composing Position<Vector> positionComp = compose(position,positionInv); Orientation<Rotation> orientationComp = compose(orientation,orientationInv); Pose<KDL::Frame> pose1Comp = compose(pose1,pose1Inv); Pose<Vector,Rotation> pose2Comp = compose(pose2,pose2Inv); LinearVelocity<Vector> linearVelocityComp = compose(linearVelocity,linearVelocityInv); AngularVelocity<Vector> angularVelocityComp = compose(angularVelocity,angularVelocityInv); geometric_semantics::Twist<KDL::Twist> twist1Comp = compose(twist1,twist1Inv); geometric_semantics::Twist<Vector,Vector> twist2Comp = compose(twist2,twist2Inv); Torque<Vector> torqueComp = compose(torque,torqueInv); Force<Vector> forceComp = compose(force,forceInv); geometric_semantics::Wrench<KDL::Wrench> wrench1Comp = compose(wrench1,wrench1Inv); geometric_semantics::Wrench<Vector,Vector> wrench2Comp = compose(wrench2,wrench2Inv);;
If you execute the program you will get screen output on the semantic correctness (and mark: in this case also incorrectness) of the compositions (if not check the build flags of your geometric_semantics library as explained in the user guide. You can print and check the result of the composition using:
// print the composed objects std::cout << "-----------------------------------------" << std::endl; std::cout << "Composed objects: " << std::endl; std::cout << " " << positionComp << " is the composition of " << position << " and " << positionInv << std::endl; std::cout << " " << orientationComp << " is the composition of " << orientation << " and " << orientationInv << std::endl; std::cout << " " << pose1Comp << " is the composition of " << pose1 << " and " << pose1Inv << std::endl; std::cout << " " << pose2Comp << " is the composition of " << pose2 << " and " << pose2Inv << std::endl; std::cout << " " << linearVelocityComp << " is the composition of " << linearVelocity << " and " << linearVelocityInv << std::endl; std::cout << " " << angularVelocityComp << " is the composition of " << angularVelocity << " and " << angularVelocityInv << std::endl; std::cout << " " << twist1Comp << " is the composition of " << twist1 << " and " << twist1Inv << std::endl; std::cout << " " << twist2Comp << " is the composition of " << twist2 << " and " << twist2Inv << std::endl; std::cout << " " << torqueComp << " is the composition of " << torque << " and " << torqueInv << std::endl; std::cout << " " << forceComp << " is the composition of " << force << " and " << forceInv << std::endl; std::cout << " " << wrench1Comp << " is the composition of " << wrench1 << " and " << wrench2Inv << std::endl; std::cout << " " << wrench2Comp << " is the composition of " << wrench1 << " and " << wrench2Inv << std::endl;
| Attachment | Size |
|---|---|
| myThirdApplication.cpp | 7.63 KB |
Some extra examples
In case you are looking for some extra examples you can have a look at the geometric_semantics_examples package. So far it already contains an example showing the advantage of using semantics when integrating twists, and when programming two position controlled robots.